NC

세이버메트릭스를 기반으로 야구 경기를 더 재미있게 관람할 수 있도록 도와드리는 ‘야구 데이터 분석’!

그동안 여러 회에 걸쳐 기본적인 야구 지표들과 BABIP의 개념, 존 통제력 스탯에 대해 설명을 드렸는데요. 이번 시간에는 팀 득점과 실점, 그리고 기대 승률의 관계에 대해 이야기해보려 합니다.

야구 경기의 승패는 어떻게 결정되나요? 네, 잘 아시다시피 득점이 실점보다 많으면 이깁니다. 간단하지요.

그럼 이런 상상을 할 수도 있겠습니다. “득점과 실점으로 승률을 설명할 수 있지 않을까?”

남다른 직관과 뛰어난 상상력으로 수많은 세이버메트릭스 개념들을 만들어 낸 빌 제임스(Bill James) 역시 이런 생각을 했고, 결국 기대 승률을 구하는 계산식을 탄생시킵니다.

예를 들어, 2016 시즌의 NC 다이노스는 857점을 득점하고, 690점을 실점했는데요.

빌 제임스는 구단의 진짜 경기력(quality)을 득점/실점 비율로 알 수 있지 않을까 생각했습니다. 즉, 2016년 NC 다이노스의 진짜 경기력은 857/690 = 1.242가 됩니다.

이번에는 나머지 팀들의 관점에서 생각해 봅시다. 2016년 NC 다이노스와의 경기에서, 다른 팀들은 합쳐서 690점을 득점하고, 857점을 실점한 셈이 되지요. 상대팀들의 평균적인 진짜 경기력을 똑같이 구해 보면 690/857 = 0.805가 됩니다.

빌 제임스는 여기서 상상력을 한 번 더 발휘해서, 팀의 기대 승률은 진짜 경기력의 비율로 나타낼 수 있지 않을까 하는 생각을 했습니다. 즉, 위의 NC 다이노스가 나머지 9팀과 골고루 경기를 치르게 되면, 아래와 같은 식으로 기대 승률을 구할 수 있을 거라고 생각한 거죠.

그래서 NC 경기력 1.242와 나머지 9팀 경기력 0.805를 대입하면,

빌 제임스 식으로 구한 NC 다이노스의 기대 승률은 60.7%가 됩니다.

이제 이 과정을 수식으로 표현해 보겠습니다.

위의 예에서 NC 다이노스의 득점을 RS(Runs Scored), 실점을 RA(Runs Allowed)라고 하면, 맞대결한 경기에서 상대팀들의 득점은 다이노스의 실점이 되므로 RA와 같고, 상대팀들의 실점은 다이노스의 득점이므로 RS와 같게 되지요.

그래서 다이노스의 진짜 경기력은 RS/RA, 나머지 상대팀들의 진짜 경기력은 RA/RS가 되고, 다이노스의 기대 승률은 아래와 같이 구할 수 있습니다.

여기서 분자와 분모를 정리하면,

이렇게 팀 득점과 실점만 가지고 기대 승률을 구하는 식이 탄생합니다.

여기서 빌 제임스가 또다시 위대한 상상력을 발휘해서, 이 식에 ‘피타고리언 기대 승률(Pythagorean Expectation)’이라는 멋진 이름을 붙여서 발표합니다.

빌 제임스는 이 식이 직각삼각형의 빗변의 제곱이 두 직각변의 제곱의 합과 같다는 ‘피타고라스의 정리’와 비슷하게 보인다고 느껴서, 이런 이름을 붙이게 되었는데요.

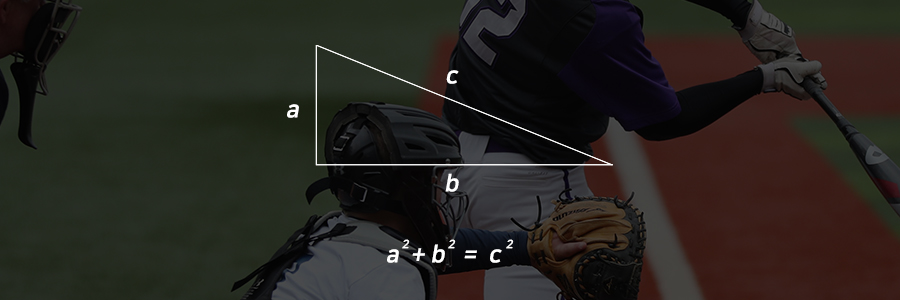
여러분이 보기엔 어떠신가요? 위의 피타고라스 정리와 빌 제임스의 식이 비슷해 보이시나요? 저는 솔직히 하나도 비슷해 보이지 않습니다만, 빌 제임스 님이 그렇다고 하시면 그런 겁니다. ^^

이름을 잘 붙였고, 실제로도 그럴 듯한 승률 예측력을 보여준 덕에, 이 식은 빌 제임스의 최대 히트상품 중 하나가 되었답니다. 만약 이 식이 ‘야구 팀의 승률에 대한 득실 정리’처럼 재미없고 긴 이름을 가지고 있었다면, 이렇게 유명해질 수 있었을까요?

기대 승률의 계산에 대한 이야기는 다음 편에서 계속 됩니다.