NC

세이버메트릭스를 기반으로 야구 경기를 더 재미있게 관람할 수 있도록 도와드리는 ‘야구 데이터 분석’!

이번 글에서는 빌 제임스(Bill James)가 만든 ‘피타고리언 기대 승률’을 보완하기 위해 탄생한 여러기대 승률 계산식에 대한 이야기를 들려드리겠습니다.

지난 글에서는 빌 제임스가 야구 팀의 진짜 경기력을 팀 득점/실점 비율로 가정하고, 아래와 같은 기대 승률 계산식을 유도하는 과정을 보여 드렸는데요. (RS = 팀 득점, RA = 팀 실점)

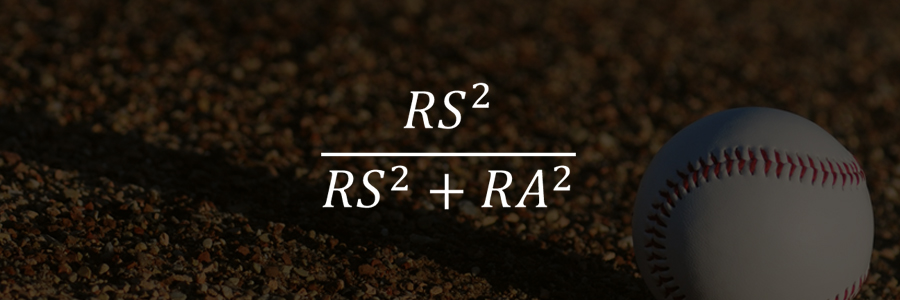
그런데 이 식이 엄밀한 수학적 증명을 통해 나온 것은 아니었죠. 빌 제임스 특유의 직관과 상상력을 바탕으로 만들어졌고, 여기에 실제 데이터를 넣어 보니 꽤 그럴싸하게 들어맞는다는 식으로 발표된 것입니다.

이러다 보니 사람들이 하나둘 의문을 갖기 시작합니다. ‘이게 최선입니까?’

사람들의 관심은 주로 지수에 모아졌는데요.

즉, 위의 식에서 x값을 어떻게 정했을 때 가장 실제 승률과 근접한 결과를 낼 수 있는지가 관건이었습니다.

90년대 후반, 컴퓨터와 인터넷이 보급되면서 많은 사람들이 이 연구에 뛰어들게 됩니다. 인터넷을 통해 입수한 메이저리그 데이터를 이용해 제각기 집에서 엑셀을 돌려볼 수 있게 된 것이죠.

실제 메이저리그 팀들의 득점-실점과 승-패 기록을 넣어서 계산해 본 결과, 사람들은 x값이 2일 때보다는 1.81에서 1.85 사이일 때 조금 더 정확도가 높아진다는 것을 발견했는데요. 이 값은 19세기 팀을 제외할지, 20세기 초의 팀을 제외할지 등 데이터의 범위를 어떻게 설정하느냐에 따라 소수점 둘째 자릿수가 바뀝니다.

그래서 베이스볼 레퍼런스 사이트는 x값을 1.83으로 하여 다음의 식을 기대 승률 계산에 적용하고 있습니다.

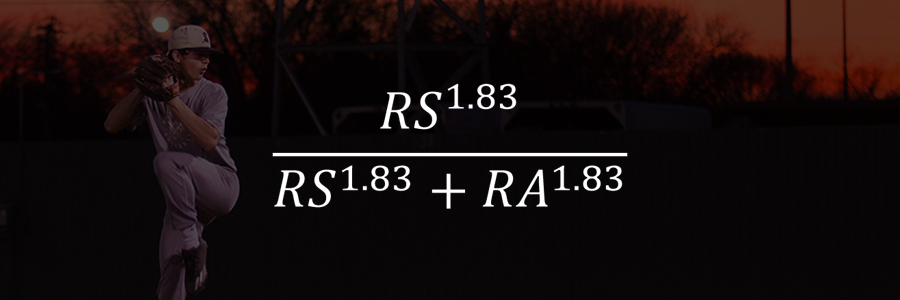
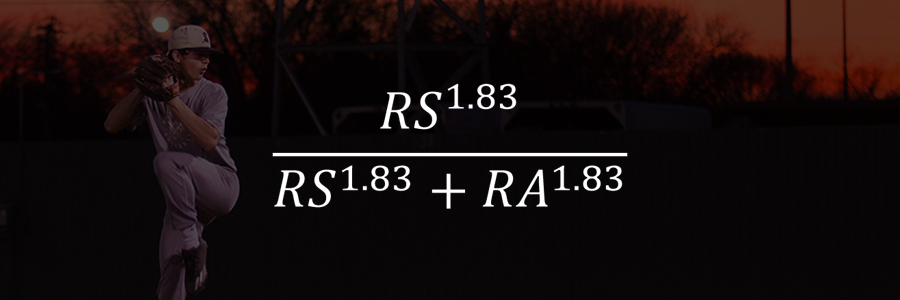
한편, x값을 바꿔서 대입하는 식으로는 이 이상 정확도를 높일 수가 없었으므로, 연구자들은 x값을 고정시키지 않고 득점, 실점의 규모에 따라 변동시키는(dynamic) 방법을 찾기 시작했습니다.

Baseball Prospectus 사이트의 설립자 중 한 사람으로도 유명한 세이버메트리션 클레이 대번포트(Clay Davenport)는 x값에 로그함수를 도입하여 정확도를 높입니다. (G = 경기 수) 이 식은 그의 이름을 따서 ‘Pythagenport’라는 명칭으로 불리게 됩니다.

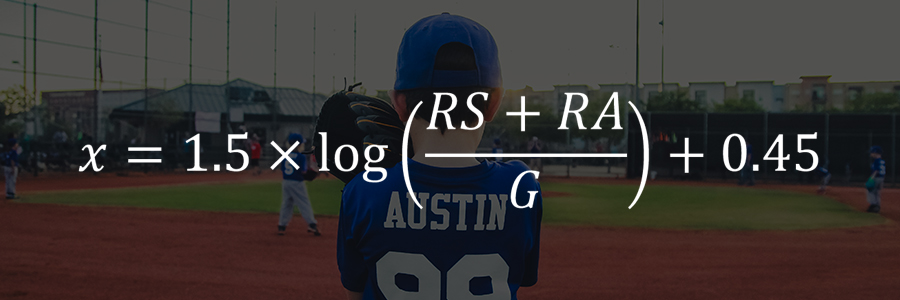
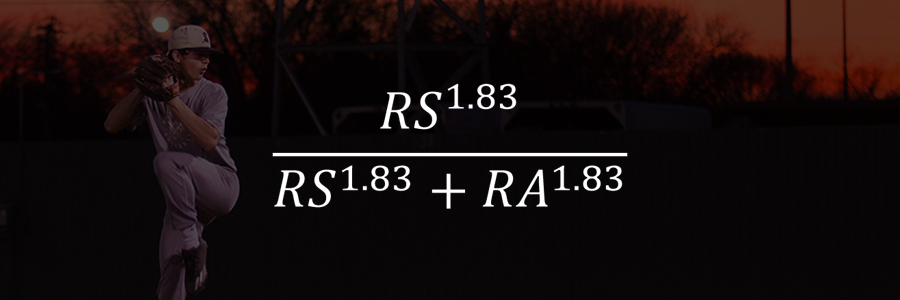
또 다른 세이버메트리션들인 데이비드 스비스(David Smyth)와 필명 ‘U.S. Patriot’은 다음과 같은 식을 찾아냈습니다. 이 식은 Patriot의 이름에 따라 ‘Pythagenpat’이라는 별명을 가지게 됩니다.

식의 버전에 따라 0.287이 0.285나 0.29 등으로 약간씩 바뀌기도 합지만 결과는 거의 똑같습니다.

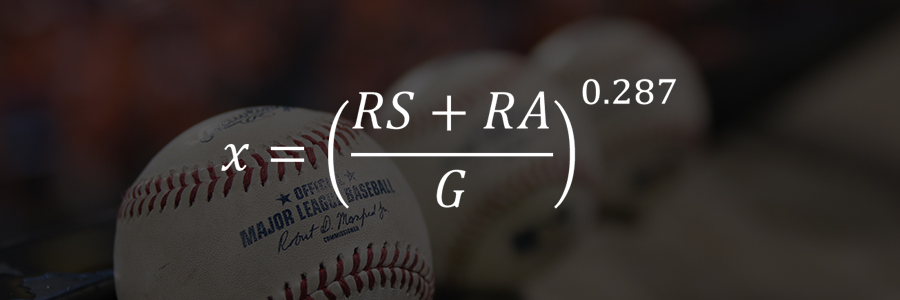
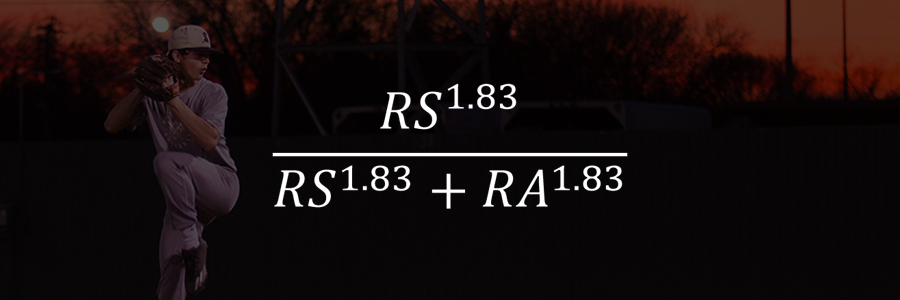
Pythagenport와 Pythagenpat, 두 식은 실제 메이저리그 데이터에서 거의 비슷한 결과를 보여줍니다만, 극단적인 경우를 상상하면 좀 달라집니다.

예를 들어, 100 경기를 해서 70 경기를 1대 0으로 이기고, 30 경기는 0대 1로 패한 팀이 있다고 해봅시다. 이 팀의 실제 승률은 .700이죠.

그런데 Pythagenport에 G=100, RS=70, RA=30을 대입하면 x값이 0.45가 되어 이 팀의 기대 승률은 0.594로 나옵니다. 한편 Pythagenpat에 똑같이 대입하면 x값은 1이 되고, 기대 승률은 .700으로 정확한 값이 나오죠.

이렇게 특정한 상황에 좀 더 잘 대응하는 Pythagenpat의 범용성이 인정받게 되었고, 현재까지 득점과 실점을 이용한 가장 정확한 기대 승률 계산식으로 남게 되었답니다.

다음 연재에서는 KBO리그의 데이터를 통해 이 식을 살펴보겠습니다.